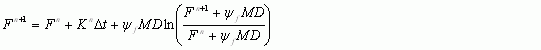Infiltration:Multi-layer Green and Ampt
While the basic Green and Ampt model has been proven effective for modeling infiltration into soils, several important common natural phenomena cause the assumption of a vertically uniform soil to be overly restrictive. Conditions such as layered soils, non-uniform initial soil moistures, surface crust, lenses, and high water tables all violate this basic assumption, yet are routinely encountered in the field. Therefore it becomes necessary to deal with these situations in some manner. The method used can have significant, if not overwhelming, effects on the hydrograph produced. This section discusses a methodology to incorporate a three layered soil profile into the GSSHA hydrologic model using Green-Ampt infiltration. Layering in soil may also be simulated with the Richards’ equation, Section 7.1.
In GSSHA v5 and above, the multi-layer GA model can be used in continuous mode, as well as with groundwater and in simulated constituent transport, including soils.
7.3.1 Layered Soils
In nature, layered soils are the norm rather than the exception. Everyone is familiar with the three layer soil system consisting of a top, A, middle, B, and bottom, C, horizon (Figure 9). Typically, soils in the A horizon are loose and high in organic material. High biological activity increases the porosity and hydraulic conductivity of soils in this layer. Soils in the B horizon are typically less permeable, with lower organic content and reduced biological activity. Soils in the C and lower horizons tend to be even less permeable, with minimal biological activity. What is found in the field could vary greatly from this simple model. Erosion and sedimentation, both recent and in geologic time frames, can cause very different layering effects. This can result in layers that become more porous with depth, or alternating porous and impermeable layers. Also, thin impermeable surface crusts can exist where compaction, raindrop impact or tillage occurs.
Regardless of the layering, when a wetting front moves from one layer to the next, the infiltration rate will be reduced. This is true regardless of the orientation of the layering. If a wetting front moves from a more porous to a less porous layer, the infiltration is reduced due to the reduced hydraulic conductivity. If the wetting front moves from a less porous layer to a more porous layer, the reduced wetting front suction causes the reduction in the infiltration rate. If the soils making up the lower layers are much coarser than the top layers, the wetting front may become unstable, and infiltration will be greatly reduced.
In a single layer infiltration model, the effect of layering must be addressed in some manner. Two possible approaches are: 1) use the properties of the top soil to represent the entire column, or 2) use some type of average values based on the depths of the layers.
7.3.2 Varying Moisture Contents
Soils do not have to be layered to cause problems with the Green-Ampt assumption of uniform soil properties. Soil moisture can also vary with depth. The variation in soil moistures with depth could be caused by layering or due to other reasons, such as interaction with the ground water table. In the latter case, the soil will tend to be driest at the surface and saturated near the water table. During periods of evaporation, the soil moisture content may vary considerably with depth. This type of condition can be roughly approximated with the three soil layer model, where the only parameter that changes through the layers is the initial soil moisture.
7.3.3 Model Formulation
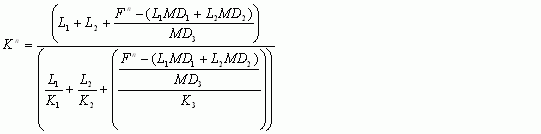
For GA infiltration in GSSHA, infiltration occurs in what is assumed to a uniform soil profile with constant hydraulic parameters and initial soil moisture throughout the profile. The Green-Ampt routine has been expanded to allow for three different soil layers to be modeled. These layers can be of any thickness and hydraulic parameters. The assumption of a sharp wetting front still applies. As the wetting front crosses the layers there is assumed to be an instantaneous change in the initial moisture, porosity, and wetting front suction head. However, the effective hydraulic conductivity is calculated at each time step based on the depth of the leading edge of the wetting front. The hydraulic conductivity, K (cm/hr), is calculated as the harmonic mean of the wetted layers. While the front is contained in the first layer, the hydraulic conductivity at any time n, Kn, is equal to K1, the hydraulic conductivity of the A soil horizon.
After the wetting front passes into the second layer, the hydraulic conductivity is defined as:
where:
- L1=thickness of the A horizon (cm),
- L2=thickness of the B horizon (cm),
- MD1=moisture deficit of the A horizon (dimensionless),
- MD2=moisture content of the B horizon (dimensionless),
- K1=saturated hydraulic conductivity of the A horizon (cm/hr),
- K2=saturated hydraulic conductivity of the B horizon (cm/hr), and
- Fn= cumulative infiltration at the n time level (cm).
The moisture content MD is defined as the effective porosity θs minus the initial moisture content θi.
When the wetting front reaches the third layer, the effective hydraulic conductivity becomes:
where MD3 (cm), and K3 (cm/hr) are the moisture content and hydraulic conductivity, respectively, of the third soil layer.
Therefore the change in effective hydraulic conductivity is gradual, as would be expected in nature. The soil is assumed to be saturated at all points behind the wetting front.
The cumulative infiltration at the n+1 time level is (Adapted from Chow et al., 1988)
where: ![]() ƒ, the wetting front suction head, and MD are for the layer containing the leading edge of the wetting front. This equation is solved iteratively by the Newton Raphson method. Once the cumulative infiltration is determined the infiltration rate, ƒ(cm/hr) is calculated by
ƒ, the wetting front suction head, and MD are for the layer containing the leading edge of the wetting front. This equation is solved iteratively by the Newton Raphson method. Once the cumulative infiltration is determined the infiltration rate, ƒ(cm/hr) is calculated by
Actually, for this method the calculation of the effective hydraulic conductivity lags the calculation of the infiltration by one time step. However, since the time steps for GSSHA are small, on the order of 1 minute, this should present minimal concern, because the hydraulic conductivity will change very little over such a short period.
In the case where rainfall rate is limiting, the cumulative infiltration is calculated as
where: dn+1 is the depth of water ponded on top of cell before infiltration is calculated.
The infiltration rate is then
7.3.4 Inputs
The multi-layered GA input represents an intermediate step in transforming from a map based input system to an index map and table based input system. The multi-layer GA approach is selected by placing the INF_LAYERED_SOIL card in the project file. Multi-layer GA requires the same inputs as the traditional GA approach except that the information must be specified in a table for all three layers. The table is specified with the SOIL_LAYER_INPUT_FILE card. This table is referenced to an index map that contains a unique integer number, starting with 1, for each soil type in the watershed. This GRASS ASCII map is specified with the SOIL_TYPE_MAP project card. The soil layer input file contains the number of soils on the first line, followed by the soil number and parameter values for each soil in the table. Soil numbers should start with soil 1 and increase monotonically. Every soil number in the table should correspond to a number in the SOIL_TYPE_MAP.
In GSSHA version 5.0 and above, the multi-layer GA model has been modified to work in long term simulation mode. The multi-layer GA model can also be coupled to saturated groundwater, and can be using in contaminant modeling, including simulation of contaminants in the soil column. The input table for the multi-layer GA model reflect these changes.
As shown below, values in the table are separated by spaces or tabs, not commas:
|
Total # of Soils |
Where: Ks is the saturated soil hydraulic conductivity (cm hr-1),
λ is the pore distribution index,
Sf is the moisture front suction head (cm),
θ is the soil moisture (fraction of total): e - saturated, f - field capacity, wp - wilting point, r - residual, i - initial,
and d is the layer depth (cm).
The numbered subscripts refer to the soil layer number, 1 – top layer, 2 – middle layer, 3 – bottom layer.
For a watershed with three soil types, soil one a uniform clay, soil two a uniform sand, and soil three a sand with an embedded clay layer, the table might look like:
|
3 |
The corresponding SOIL_TYPE_MAP would contain the integers 1, 2 and 3 corresponding to the locations of the soils 1, 2, and 3 in the SOIL_LAYER_INPUT_FILE.
Newer versions of GSSHA, 5.7 and above, support the multi layer inputs in the MAPPING_TABLE_FILE. For these versions the inputs can be included as stated above, or more effciently, included in the MAPPING_TABLE_FILE. In this case, the above inputs are put into the MULTI_LAYER_SOIL table, as shown below. The inputs and the format are the same as above. WMS v9.0 and above support this ability. The table below was developed with WMS v9.1. It should be noted that the term BUB_PRESS is actually the wetting front suction head Sf.
|
MULTI_LAYER_SOIL "hawaii_Soil_final" |
GSSHA User's Manual
- 7 Infiltration
- 7.1 Richards’ Equation
- 7.2 Green and Ampt (GA)
- 7.3 Multi-layer Green and Ampt
- 7.4 Green and Ampt with Redistribution (GAR)
- 7.5 Parameter Estimates