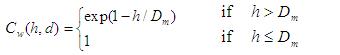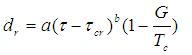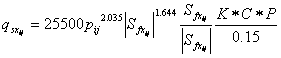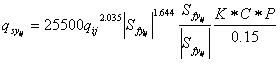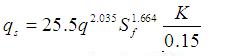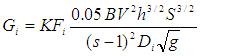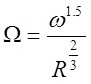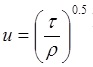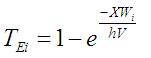Soil Erosion:Overland Erosion Formulation
Contents
10.1.1 Overland Erosion Controlling Equation
The overland sediment routing is based on a two-dimensional mass balance equation,
where h = water depth (m); c = sediment concentration (kg m-3); t = time (s), qx and qy = unit discharge in x- and y-directions, respectively (m2/s); and e(x,y,t) = sediment source/sink (kg m-2• s-1); qz(x,y,t)=lateral sediment inflow to the channels (m-2 s-1). e(x,y,t) consists of two major sources, namely, soil detached by raindrop impact and soil detached by surface runoff (or deposition):
where di=soil detachment by rainfall impact (kg m-2• s-1) and dr=soil detachment by surface runoff (kg m-2• s-1).
10.1.2 Detachment of Overland Sediment Particles
Detachment of overland sediment particles occurs due to two processes, detachment by rainfall impact, and detachment by surface runoff.
10.1.2.1 Detachment by Rainfall Impact
Following a similar approach presented by Wicks and Bathurst [1996] and Gabet and Dunne [2003], detachment by raindrops is considered to be a function of rainfall intensity. Raindrop detachment also takes into account factors such as “cushioning” by ponded surface water, ground cover, and plant interception.
where di = detachment capacity rate (kg m-2 s-1), KI = soil erodibility factor for detachment by raindrop impact (J-1), Cw = water depth correction factor, CG = canopy cover factor, Ci = a cover-management factor, I = rainfall intensity (mm h-1), and β = empirical coefficient related to rainfall intensity.
The calculation of water depth correction factor is based on the assumption that surface water depths greater than a critical depth protect the soil from raindrop impact erosion Wicks and Bathurst [1996]. The expression for the correction factor, Cw, is,
where h = water depth (m), and Dm = median raindrop diameter (m). The median raindrop diameter is determined from the Laws and Parsons [1943] equation:
10.1.2.2 Surface Runoff Detachment
Surface runoff detaches soil particles by exerting a shear stress that breaks the bonds between particles. Erosion in rills is lumped and described as gross rill erosion. Within a grid cell, rill erosion and flow are assumed to be uniformly distributed. The detachment capacity rate by surface runoff has the form:
where: dr = detachment capacity rate (kg m-2•s-1), a and b are empirical coefficients, τ = the flow shear stress (Pa), τcr is the critical shear stress, G is the sediment load (kg m-2 s-1), and Tc is the sediment transport capacity of surface runoff (kg m-2 s-1). In the WEPP model, b is assumed equal to 1.0. Equation 101 provides an upper limit on the rate at which sediment that can be taken up by flowing water.
10.1.3 Sediment transport capacity of surface runoff
Transport of sediments on the overland flow plane is constrained by the ability of the water to carry sediments. Many researchers have investigated the process and have identified multiple equations that can be used to calculate this carrying capacity of the overland flow. Several of these have been implemented in GSSHA.
10.1.3.1 Kilinc Richardson Equation
Kilinc and Richardson studied the mechanics of overland soil erosion at Colorado State University Engineering Research Center in a flume 1.2 m deep, 1.5 m wide, and 4.9 m in length. Their investigation resulted in a sediment transport equation of uniform flow sheet and rill erosion on bare sandy soil. The original one-dimensional Kilinc-Richardson (1973) equation is:
where: the factor 25,500 is an empirical constant, ![]() is the sediment unit discharge (ton m-1 s-1) and q and So have previously defined. The form of Equation 102 is consistent with many sediment transport predictors, as reviewed by Julien and Simons (1985).
is the sediment unit discharge (ton m-1 s-1) and q and So have previously defined. The form of Equation 102 is consistent with many sediment transport predictors, as reviewed by Julien and Simons (1985).
Julien (1995) modified the original Kilinc-Richardson equation to expand the applicability of the equation to non-uniform flow with consideration of soil and land-use specific factors:
where: K = soil erodibility factor, with values ranging from 0 to 1, C = soil cropping factor (0-1), and P = conservation factor (0-1).
The K, C and P factors are empirical coefficients with the same conceptual meaning as those used in the Universal Soil Loss Equation (Renard et al., 1991). The factor 0.15 in the denominator represents the maximum erosivity of the sand used in the original flume experiments. Equation 103 is applied within each model grid cell in two dimensions, which allows separate calculations of the potential sediment transport rate in the x- and y-directions:
with Sƒx and Sƒy defined using Equation 2, and p and q calculated using Equations 6 and 7, respectively.
The numerical approach in the current version of GSSHA is to apply the modified Kilinc and Richardson equations 104 and 105 to determine potential transport of sediment within each grid cell. The methodology is explained in detail in Johnson (1997) and Johnson et al. (2000). The potential sediment discharge in each of the two flow directions in each grid cell is calculated using the following two equations:
and,
In the current version of GSSHA, the three erosioin parameters K, C, and P, have been replaced with a single erosion parameter K, which represents the three original components, without the need to specify three different parameters for each grid cell. Reducing the number of parameters greatly facilitates calibration. The form of the equation used in GSSHA is currently:
where qs is the sediment unit discharge (kg m-1 s-1), q is the unit discharge (m3 s-1), Sf is the friction slope (-), and K is a combined factor(0-1) that consists of the combined influence of soil erodibility, vegetation, and land-use.
10.1.3.2 Engelund-Hansen Equation
The Engelund-Hansen [1967] relation is used to calculate sediment transport for each sediment size class and the resulting total transport is calculated by multiplying the proportion of the size in the parent material by the calculated rate.
where Gi is the volumetric sediment transport rate of ith size fraction (m3 s-1), K is the calibration coefficient (=1 for standard equation) (-), Fi is the proportion of i-th faction in the parent material or deposited layer (-), B is the width of flow (m), V is the mean water velocity (m s-1), h is the flow depth (m), S is the water surface slope (-), s is the specific gravity of ith fraction (-), and g is the gravitational acceleration (m s-2), is the sediment density (kg m-3), is the water density (kg m-3), Di is the mean size of i-th fraction (m). The factor 0.05 in the equation was developed from empirical data.
The suggested applicability of the Engelund-Hansen equation is for, where "DN" is the grain size for which N% of sediment is finer by weight, and for sand-size sediments coarser than 0.15 mm.
10.1.3.3 Stream Power Approach
Several stream power methods [Everaert 1991] can also be chosen to calculate the transport capacity of surface runoff. The general expression has the form:
where a is the transport coefficient, b is an exponent, ω = steam power; ωc=a critical stream power. Prior to version 5.7 these values were specified by the user. For versions 5.7 and beyond the exponents are assigned based on literature values [Everaert 1991]. These there parameters are no longer input in the cmt input table file.
10.1.3.4 Median size diameter, D50 , Approach
In the versions 5.7s and beyond, the Stream Power Approach defined in 10.1.3.3, are replaced by laboratory physical model imperical equations derived by Everaert [1991] which are based on the sediment particle median size diameter, D50. The replacement is done to reduce the number of calibration parameters, a, b and critical values defined in sec. 10.1.3.3.
The followings are the list of methods and their respective equations:
a) Effective stream power method:
where,
and <math>q_s</math> = sediment unit discharge (kg/ m/ sec)
<math>D50</math> = Grain size parameter (um)
<math>\Omega</math> = effective stream power
<math>\omega</math> = stream power (N/m/s)
<math>R</math> = flow depth (m)
<math>q</math> = unit discharge (m2/s)
<math>S_f</math> = friction slope (m/m)
<math>\rho</math> = density of water at 20 C (kg/m3)
<math>g</math> = gravitational acceleration
This method is implemented if 4 is used for the project card SOIL_EROSION.
b) unit stream power method:
where, <math>Vel</math> = velocity (m/s)
<math>S_f</math> = friction slope (m/m)
<math>q_s</math> = sediment unit discharge (kg/ m/ sec)
<math>D_{50}</math> = Grain size parameter (um)
This method is implemented if 3 is used for the project card SOIL_EROSION.
c) slope and unit discharge method:
if(d50<33.0)
else if(d50>=33.0 && d50<61.0)
else if(d50>=61.0 && d50<122.0)
else if(d50>=122.0 && d50<190.0)
If(d50>190.0)
This method is implemented if 5 is used for the project card SOIL_EROSION.
d) Transport capacity by shear velocity method:
u = shear velocity (m/s)
Τ = shear stress (N/m2)
if(d50<33) and if(u>1.4)
if(d50>=33.0 && d50<61.0) and if(u>1.4)
if(d50>=61.0 && d50<122.0) and if(u>1.45)
if(d50>=122.0 && d50<190.0) and if(shear_vel>1.55)
if(shear_vel>1.8)
In the above equations, D50 and all other physically based hydrological, topographical and geomorphological parameters are defined by GSSHA model and need not be calibrated. As these methods are solely based on the experimental flume scale of 5 x 30 cm and 12 x 100 cm, the applicability of these lab model scale based imperical relations has been tested on catchment scale and a product of ‘constant factor’ and ‘adjustment factor’ is applied as a multiplier to each equation (a – d) in this section. Adjustment factor is a parameter for calibrating the individual equations. Constant factor is used to confine the bound of adjuistment factor between 0 and 1 while calibrating. Constant factor for each method is hard coded. We are currently assessing these methods. All of them may not appear in the next release version.
10.1.4 Deposition rate
When the sediment transport capacity is insufficient to transport the sediment in suspension within a grid cell, sediment is deposited. Sediment deposition in each grid cell is calculated for each size fraction using a trap efficiency relation [Johnson et al., 2000]:
where: TEi is the trap efficiency for the ith size fraction, X is the width of the grid cell (m), Wi is the fall velocity of the ith size fraction (m s-1), h is the overland flow depth (m), and V is the overland flow velocity (m s-1). The trap efficiency is a number between 0 and 1, which is assumed equal to the fraction of suspended sediment in each size fraction that is deposited in the grid cell. The use of trap efficiency forces larger particles to deposit before smaller particles.
GSSHA User's Manual
- 10 Soil Erosion
- 10.1 Overland Erosion Formulation
- 10.2 Channel Sediment Transport Formulation
- 10.3 Sediment in Lake
- 10.4 Applicability of the Sediment Routing Methods
- 10.5 Simulations with Soil Erosion